
The reflect_curve function for the XYK pool sizes passive bid/ask orders without accounting for the swap fee, allowing takers to match those orders effectively fee-free. This under-collects fees that should accrue to liquidity providers, causing direct LP losses in addition to normal impermanent loss.
In dango/dex/src/core/xyk.rs, the total order size at price p is computed from the reserves as if there were no swap fee. For bids, the size uses quote_reserve / p - base_reserve; for asks, it uses base_reserve - quote_reserve / p. The fee factor (1 - swap_fee) is omitted, so passive orders are reflected at sizes that do not accrue the fee when taken.
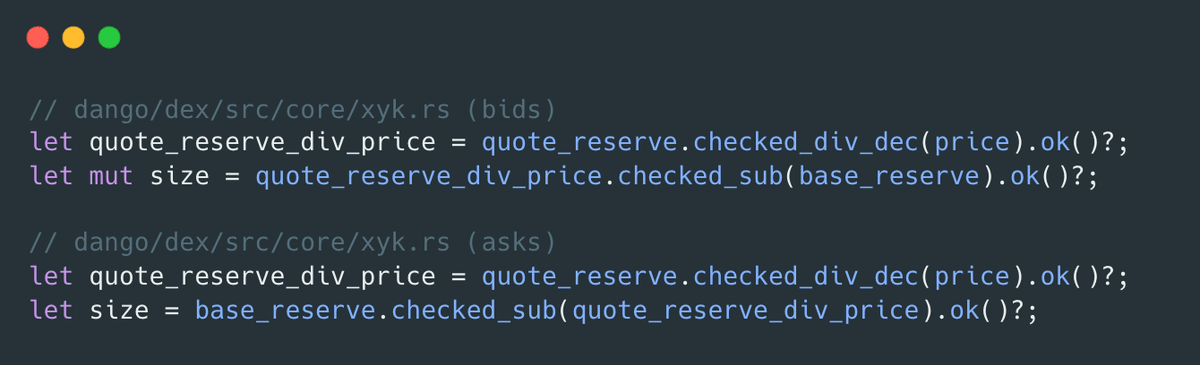
Mathematically, for a bid at price p with reserves R_b and R_q and fee f, the equality s * p = (R_q * s)/(R_b + s) * (1 - f) yields s = R_q * (1 - f) / p - R_b. The implementation lacks the (1 - f) term. A symmetric adjustment is required for asks as well.
Detailed derivation
Note: not needed for the sake of understanding this issue, but still nice to go through.
Bids (pool buys base, taker sells base):
Reserves: R_b (base), R_q (quote); price p (quote per base); fee f.
Exact-in (base in) output after fee: Q_out = (R_q * s) / (R_b + s) * (1 - f).
Passive bid at price p promises s * p quote for s base: set s * p = Q_out.
Solve: p = (R_q / (R_b + s)) * (1 - f) ⇒ R_b + s = R_q * (1 - f) / p ⇒ s = R_q * (1 - f) / p - R_b.
Therefore total size at price p must be Rq*(1-f)/p - Rb.
Asks (pool sells base, taker buys base):
Taker pays quote x = s * p, wants to receive s base.
Exact-in (quote in) output after fee: B_out = (R_b * x) / (R_q + x) * (1 - f).
Set s = B_out with x = s * p:
s = (R_b * s * p) / (R_q + s * p) * (1 - f) ⇒ 1 = (R_b * p) / (R_q + s * p) * (1 - f).
Hence R_q + s * p = R_b * p * (1 - f) ⇒ s * p = R_b * p * (1 - f) - R_q ⇒ s = R_b * (1 - f) - R_q / p.
Therefore total size at price p must be Rb*(1-f) - Rq/p.
Alpha: always make sure fees are charged in all scenarios, if not sure, submit anyway.
Conclusion
This finding would earn you $1493, basically from missing functionality, so make sure to always think about what is missing, and not only what is wrong.
Full Report
Codebase